字母表

注意区分$\epsilon$ 和 $\varnothing$

$\epsilon$ 是一个长度为0的句子
$\varnothing$ 是空集

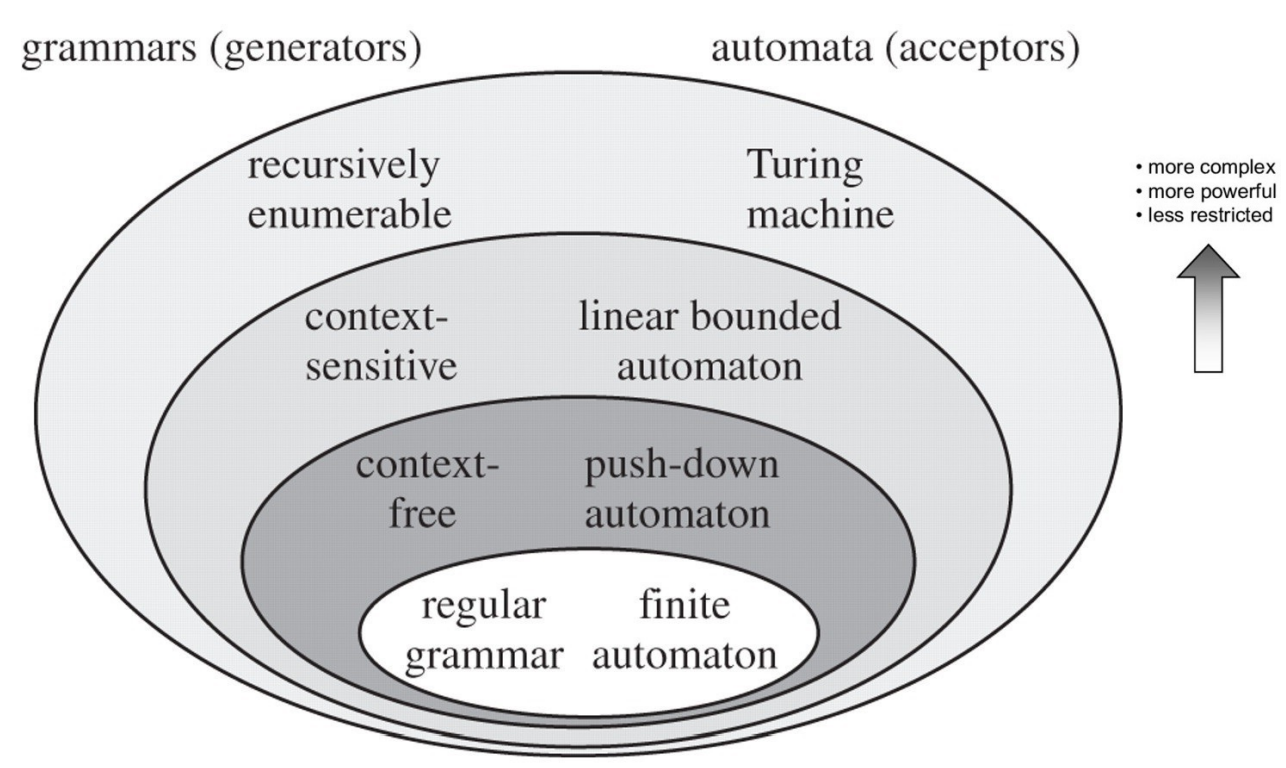
乔姆斯基文法体系

0型文法

即文法 $ G(V,T,P,S)$ 称为 短语结构文法(PSG)

1型文法

对于0型文法G有
\[ \forall \alpha \to \beta \in P, \quad |\beta| \geq |\alpha| \]
称为1型文法或 上下文有关文法(CSG)

2型文法

对于1型文法G有
\[ \forall \alpha \to \beta \in P, \quad |\beta| \geq |\alpha| 并且 \alpha \in V \]
称为2型文法或 上下文无关文法(CFG)

3型文法

对于2型文法G
\[ \forall \alpha \to \beta \in P, \quad \alpha \to \beta 具有形式\\ A \to w\\ A \to wA \]
其中 $w \in T^+$

称为3型文法或 正则文法 (RG)

文法类型	$\forall \alpha \to \beta$
0（短语结构）	无限制
1（上下文有关）	$\|\beta\| \geq \|\alpha\|$
2（上下文无关）	$\|\beta\|\geq \|\alpha\|$ 并且 $\alpha \in V$
3（正则）	$A \to w\\A \to wA$

从上到下是包含关系

正则文法最简形式

定理：L是RL充要条件是存在文法，其产生式要么形如 $A \to a$ 要么形如 $A \to aB$

线性文法

$\forall \alpha \to \beta \in P$ 均具有形式

$A \to w$
$A \to wBx$

其中 $w, x \in T^*$

右线性文法

$\forall \alpha \to \beta \in P$ 均具有形式

$A \to w$
$A \to wB$

其中 $w, x \in T^*$

左线性文法

$\forall \alpha \to \beta \in P$ 均具有形式

$A \to w$
$A \to Bw$

其中 $w, x \in T^*$

定理：左线性文法充要条件：其产生式要么形如 $A \to a$ 要么形如 $A \to Ba$

定理：左线性文法与右线性文法等价

语言识别

回溯

遍历所有的推导

有限自动机

\[ M = (Q, \Sigma, \delta, q_0, F) \]

$Q$ 状态集合
$\Sigma$ 输入字母表
$\delta$ 状态转移函数
$q_0$ 开始状态
$F$ 终止状态

DFA

每个输入字符有确定的状态转移

即时描述

$\delta (q_0, x) = q$ 那么 $xqy$ 称为一个即时描述，表示 xy是正在处理的字符串，当前到达状态q，M正准备处理y的第一个字符

$\alpha \vdash_M^n \beta$ 表示从即时描述 $\alpha$ 移动n次到达即时描述 $\beta$ ，上标同样可以使用 *、+

如果 xqay 是M的一个即时描述，且 $\delta (q, a) = p$ 那么 $xqay \vdash_M xapy$

定义：状态的字符串集合：从初始状态能引导状态机到达状态的字符串集合
\[ \text{set}(q) = \{x|x\in \Sigma^*, \delta(q_0, x)=q\} \]
定义：$R_M$ 等价关系：
\[ \forall x,y \in \Sigma^*, xR_My \Leftrightarrow \exists q \in Q \quad s.t.\\ x \in \text{set}(q) \quad \text{and} \quad y \in \text{set}(q) \]
上述是等价关系，能够将 $\Sigma^*$ 分成不多于 $|Q|$ 个等价类

NFA

与DFA等价

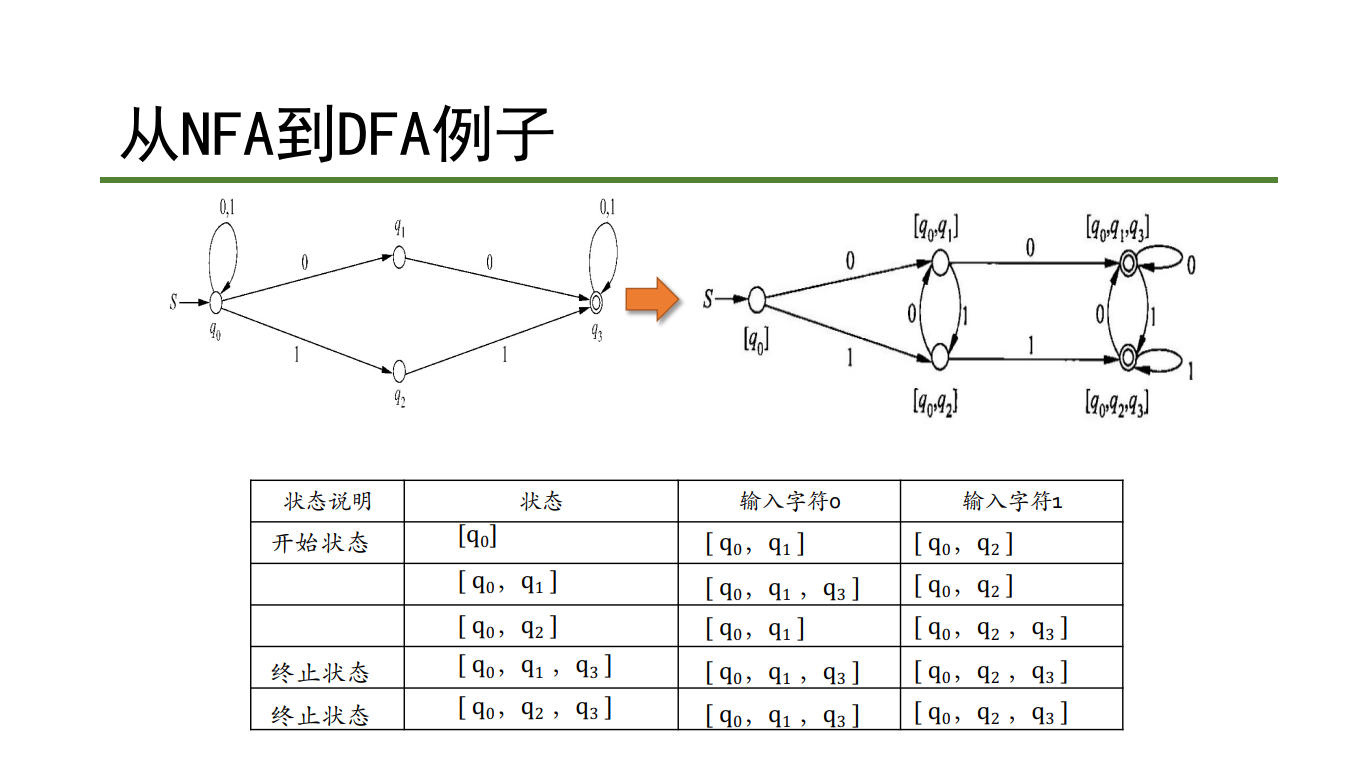
从NFA到DFA

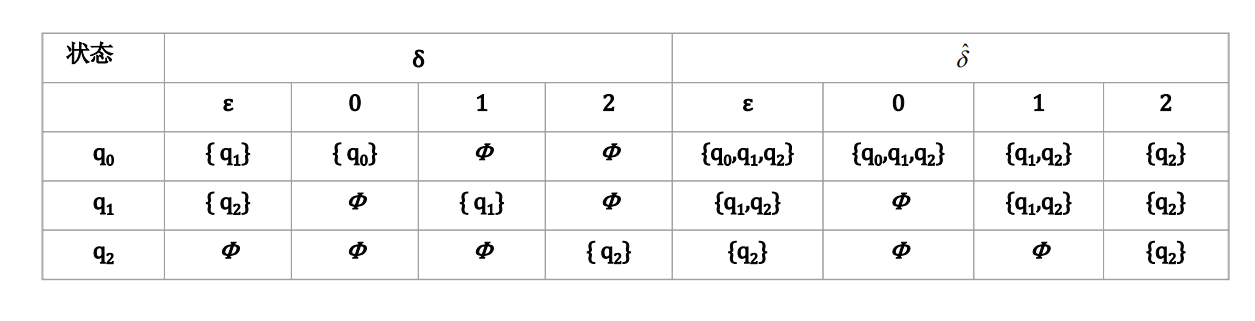
带空移动的NFA

$\epsilon$ 闭包
\[ \epsilon-\text{CLOSURE}(q) = \{p|从q到p有一条标记为\epsilon的路径\} \]
对状态集合同样也有闭包概念
\[ \hat \delta (q,a) = \hat \delta (a,\epsilon a) = \epsilon-\text{CLOSURE}(P)\\ P =\{p|\exists r \in \hat\delta(q, \epsilon) s.t. p \in \delta(r,a\} \\ = \bigcup_{r\in \hat \delta(q,\epsilon)} \delta(r,a) \]

由带空移动的NFA构造等价NFA

取NFA $M_2 = (Q, \Sigma, \delta_2, q_0, F_2)$ 其中
\[ F_2 \left\{ \begin{align} &F \cup \{q_0\} \quad &\text{如果} F\cap \epsilon-\text{CLOSURE}(q_0)\neq 0\\ &F \quad &\text{如果} F\cap \epsilon-\text{CLOSURE}(q_0)= 0 \end{align} \right. \]
对于 $\forall (q,a) \in Q \times \Sigma$ 使 $\delta_2(q,a) = \hat \delta_1(q,a)$

其实就是，写出 $\hat \delta$ 的表，把空移动去除，按照表中集合连线，再按照上述步骤判断一下终止状态都有哪些。

如

$q_0$ 的 0移动有 $q_0, q_1, q_2$ ，那么局部的NFA有

graph LR
q0((q0))
q1((q1))
q2((q2))
q0 --0-->q0
q0 --0-->q1
q0 --0-->q2

其余状态同理。

FA接收的语言是RG

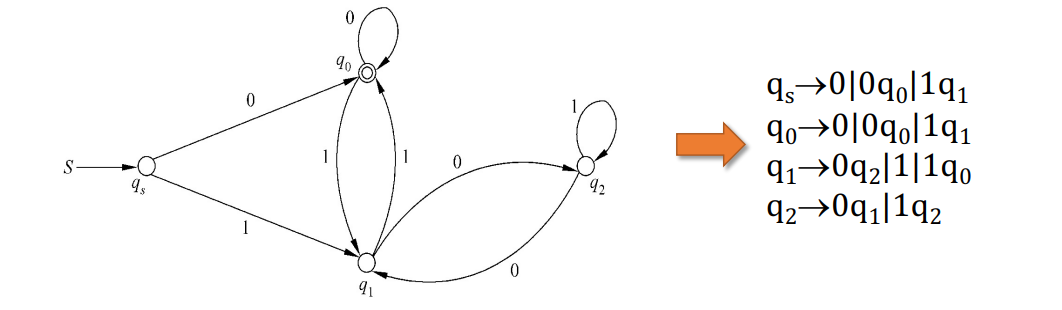
DFA转RG

构造方法
\[ P = \{q \to ap | \delta (q,a) = p\} \cup \{q \to a | \delta (q,a) = p\in F\} \]
例如：

RG转DFA

每个变量看成一个状态，

如果派生为 $A \to wB$ 的形式，那么DFA就为 A --w--> B 的形式。
如果派生为 $A \to w$ 的形式，那么DFA就为 A --w--> Z 的形式，其中Z代表终止状态。

可以用下式表示
\[ \delta(A,a) = \left\{ \begin{align} &\{B|A \to aB \in P\}\cup\{Z\} \quad &\text{if } A \to a \in P \\ \\ &\{B|A \to aB \in P\} \quad &\text{if } A \to a \notin P \end{align} \right. \]

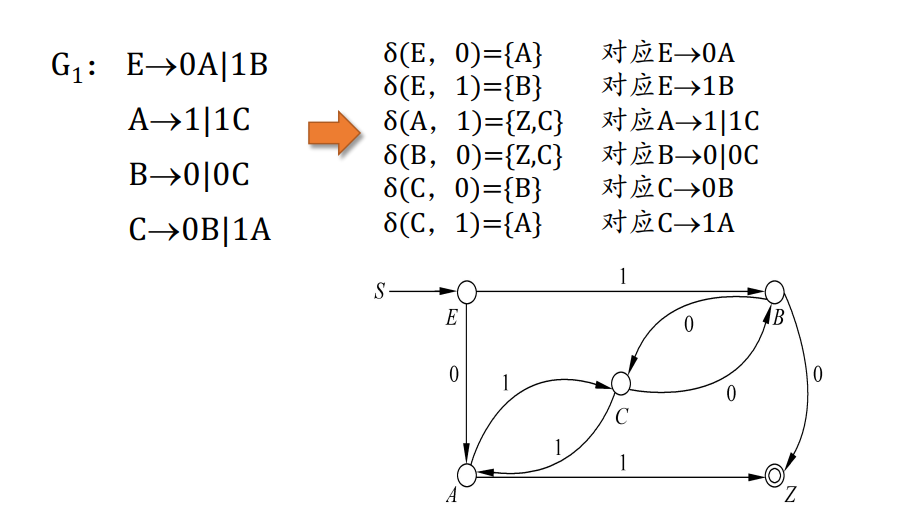
左线性文法转DFA

左线性文法 $G(V,T,P,S)$ 无空串

FA为 $M=(V\cup\{Z\}, T,\delta,Z,\{S\})$ 此处Z为初始状态
$\forall (a,B) \in T\times V$
如果 $A \to Ba \in P$ 那么 $\delta (B,a)=A$
如果 $A \to a \in P$ 那么 $\delta (Z,a)=A$

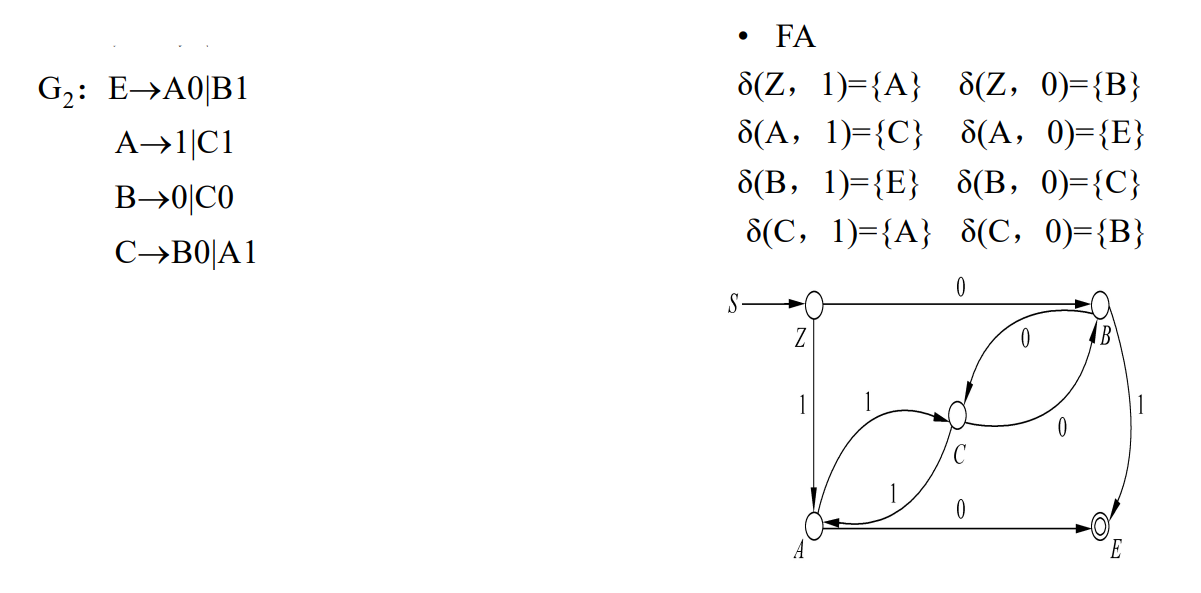
DFA转左线性文法

预处理DFA
1. 删除陷阱状态
2. 图中添加Z作为文法开始变量
3. 复制一条原本到达终止状态的弧，使其从原本状态出发到Z
构造文法
- 如果 $\delta (A,a) = B$ 则有 $B \to Aa$
- 如果 $\delta (A,a) = B$ 且A是开始状态，则有 $B \to a$

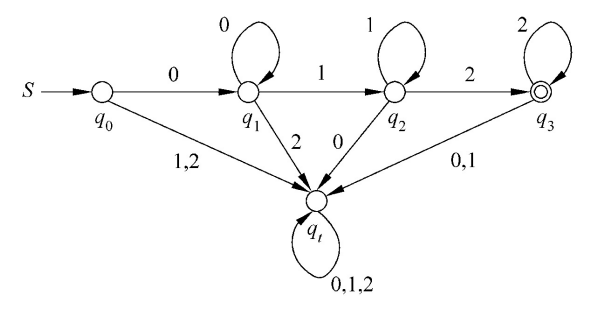
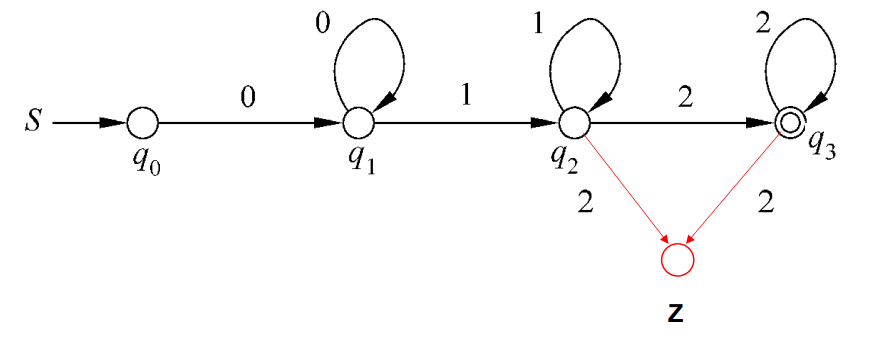
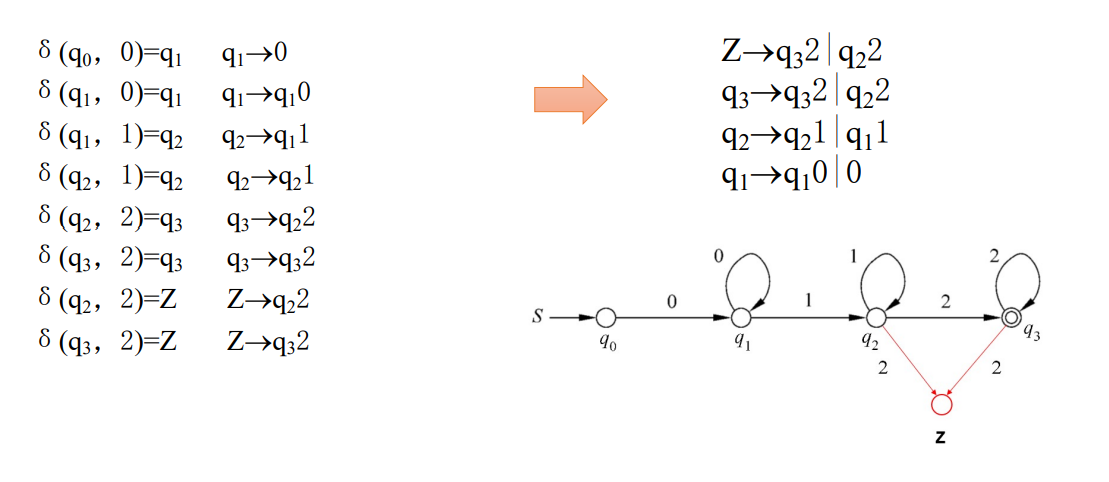
FA的变形

2DFA

\[ M = (Q,\Sigma,\delta,q_0,F) \]

$\delta: \ Q\times \Sigma \to Q \times \{L,R,S\}$

2NFA

类似2DFA

Moore机

六元组
\[ M = (Q,\Sigma,\Delta,\delta,\lambda,q_0) \]
$\Delta$ 输出字母表

$\lambda: Q \to \Delta$ 输出函数，状态 $q$ 输出对应字符

Mealy机

六元组
\[ M = (Q,\Sigma,\Delta,\delta,\lambda,q_0) \]
$\Delta$ 输出字母表

$\lambda: Q\times \Sigma \to \Delta$ 输出函数，$\lambda(q,a)=d$ 表示在状态 q 读入字符 a，输出字符d

Moore机和Mealy机等价

正则表达式

优先级：闭包>乘>加

运算律

结合律
分配律：$r(s+t) = rs+rt$
交换律：$r+s = s+r$
幂等律：$r+r=r$
零元素与空元素
- $r+\varnothing = r$
- $r\epsilon = \epsilon r = r$
- $r\varnothing = \varnothing r = \varnothing$关于这点和上一点，看二者的定义，结合分配律理解
- $L(\varnothing) = \varnothing$
- $L(\epsilon) = \{\epsilon\}$
- $L(\varnothing^*) = \{\epsilon\}$ 因为 $L(\varnothing^0) = \{\epsilon\}$
- $L((r^*s^*)^* = L((r+s)^*)$

RE与FA等价

RE转NFA

基本的例子

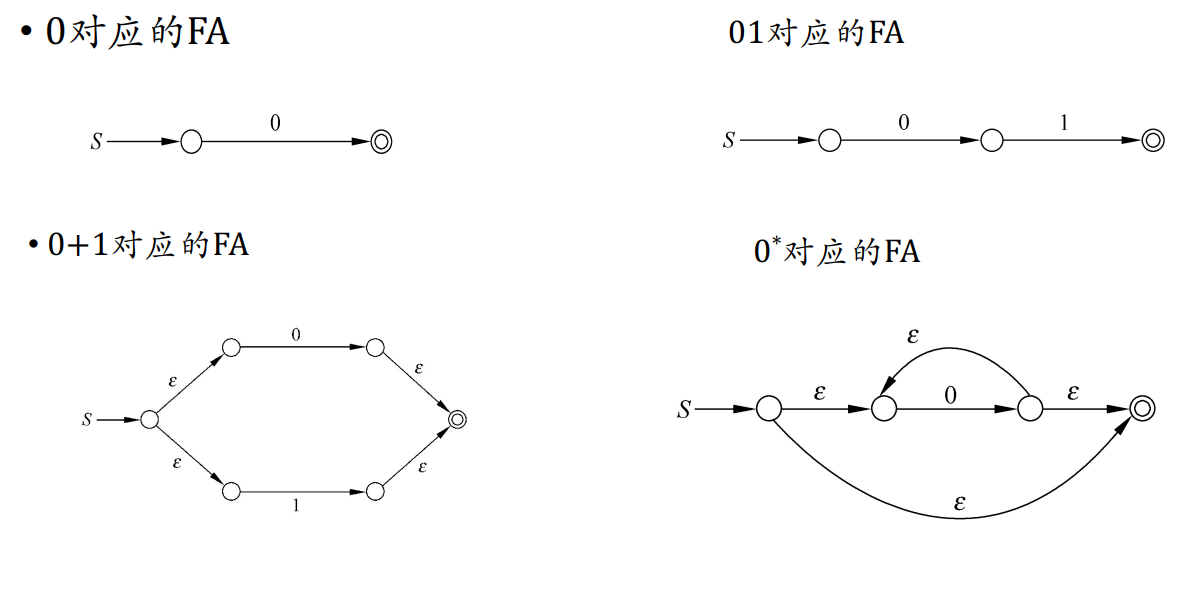
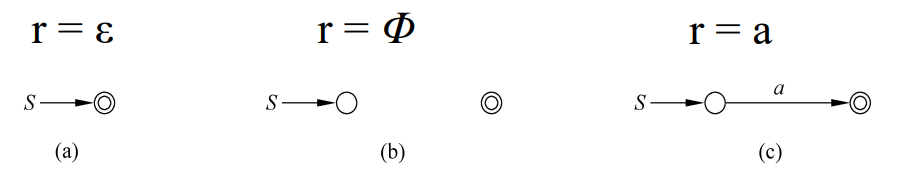
根据以上例子，给出 $r=r_1+r_2;\quad r=r_1r_2;\quad r=r_1^*$ 构造方法

加法构造

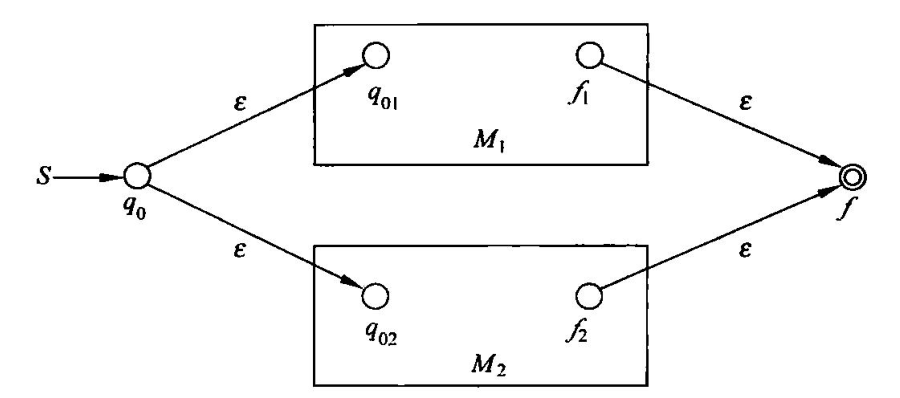
乘法构造

闭包构造

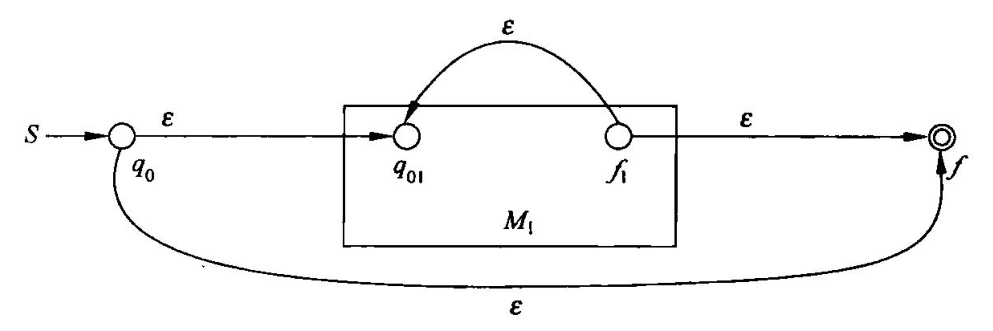
DFA转RE

预处理
- 给开始和终止加上X、Y状态
- 去掉所有不可达状态
对图操作
- 并弧：将从q到p的标记为$r_1,r_2,\cdots,r_g$并⾏弧用从q到p的、标记为$r_1+r_2+\cdots +r_g$ 的弧取代这g个并⾏弧。
- 去状态1：如果从q到p有⼀条标记为$r_1$的弧，从p到t有⼀条标记为$r_2$的弧，不存在从状态p到状态p的弧，将状态p和与之关联的这两条弧去掉，用⼀条从q到t 的标记为$r_1r_2$的弧代替。
- 去状态2：如果从q到p有⼀条标记为$r_1$的弧，从p到t有⼀条标记为$r_2$的弧，从状态p 到状态p标记为$r_3$的弧，将状态p和与之关联的这三条弧去掉，用⼀条从q 到t的标记为$r_1r_3^ *r_2$的弧代替。
- 去状态3：如果图中只有三个状态，⽽且不存在从标记为X的状态到达标记为Y的状态的路，则将除标记为X的状态和标记为Y的状态之外的第3个状态及其相关的弧全部删除。
从标记为X的状态到标记为Y的状态的弧的标记为所求的正则表达式。如果此弧不存在，则所求的正则表达式为 $\varnothing$

正则语言表示方法转化

正则语言的性质

泵引理

由于DFA中状态个数是有穷的，所以在处理⼀个足够长的句⼦的过程中，必定会重复地经过某⼀个状态。

设L为RL，那么对应有DFA $M = (Q,\Sigma,\delta,q_0,F)$ 假设有N个状态。

那么 $z = a_1a_2\cdots a_m\quad m \geq N$ 由于一共N个状态，状态序列 $q_0,q_2,\cdots ,q_N$ 有N+1状态，会有两个状态重复。不妨假设 $q_k = q_j$
$$
(q_0, a_1a_2a_k)=q_k \
(q_k, a_{k+1}a_j)=q_j = q_k \
(q_j, a_{j+1}a_m)=q_m \

因此i \
(q_k, (a_{k+1}a_j)^i) = q_j=q_k
$$
因此可以理解为 $a_1\cdots a_k (a_{k+1}\cdots a_j)^i a_{j+1}\cdots a_m \in L(M)$

设
\[ u= a_1a_2\cdots a_k\\ v = a_{k+1}\cdots a_j\\ w = a_{j+1}\cdots a_m \]
那么 $uv^iw \in L$ 由于 $k<j\leq N$ 所以 $|uv| = j \leq N, \ |v|\geq 1$

引理(泵引理)

L为RL，则存在仅依赖于L的正整数N $\forall z \in L$ 如果 $|z|\geq N$ 则存在u、v、w满足

z = uvw
$|uv| \leq N$
$|v|\geq 1$
对于任意整数 $i \geq 0 \quad uv^iw \in L$
N不大于接受L的最小DFA的状态数。

利用泵引理证明一个语言不是RL

首先假设该语言是RL，则其应该满足泵引理，选任意的N.
找到一个语言中的句子$z=L(|z|\geq N)$.
任选满足z=uvw，其中$|v| \geq 1$，且$|uv|\leq N$的u,v,w
找到一个$i\geq 0$，证明使$uv^iw\notin L$.
推出矛盾说明该语言不满足泵引理，从而说明该语言不是RL。

泵引理用来证明一个语言不是RL

不能用泵引理去证明一个语言是RL

正则语言的封闭性

定理：RL在并、乘积、闭包运算下是封闭的

定理：RL 在补运算下是封闭的。

DFA $M'=(Q,\Sigma, \delta, q_0, Q-F)$ 对应着正则语言的补集

定理：RL 在交运算下是封闭的。

正则代换

$\Sigma\quad \Delta$ 是两个字母表，映射 $f:\Sigma \to 2^{\Delta^*}$ 称为是代换，如果 $\forall a \in \Sigma \quad f(a)$是$\Delta$ 上的RL，那么称为正则代换。

先将f定义域扩展到 $\Sigma^*$ 上

$f(\epsilon) = \{\epsilon\}$
$f(xa) = f(x)f(a)$

再扩展到 $2^{\Sigma^*}$

$f(L) = \bigcup_{x\in L} f(x)$

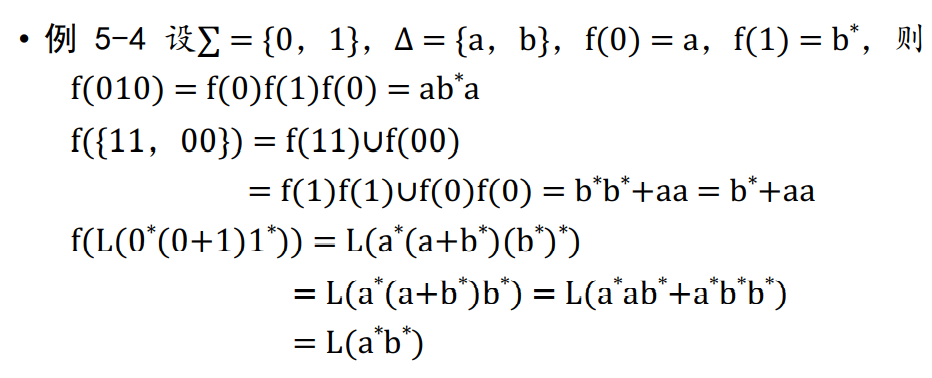
定理：L是Σ上的RL，那么正则代换f满足 $f(L)$ 也是RL

定义：对于字母表$\Sigma$和$\Delta$，$f: \Sigma \to \Delta^*$ 如果 $\forall x, y \in\Sigma^*\quad f(xy) = f(x)f(y)$ 则称为同态映射

L的同态像：
\[ \forall L \subset \Sigma^*\quad f(L) = \bigcup_{x\in L}f(x) \]
$\forall w \in \Delta^* \quad \forall L \subset \Delta^*$ 同态原像是一个集合

定义：商 $L_1/L_2 = \{x|\exists y \in L_2 \quad s.t.\ xy\in L_1\}$

主要用来考虑句子后缀

Myhill-Nerode

等价关系同样表述为 $xR_M y \Leftrightarrow \delta(q_0,x) = \delta(q_0,y)$

语言确定的等价关系： $xR_L y \Leftrightarrow (\forall x \in \Sigma^*, xz\in L \Leftrightarrow yz \in L)$；x,y后不管接什么串z，要么都是L的句子，要么都不是

右不变的等价关系：如果 $x\ R\ y$ 那么 $\forall z \in \Sigma^*$ 必有 $xz\ R\ yz$

$R_M$ 和 $R_L$ 都是右不变的。

R是 $\Sigma^*$ 上的等价关系， $\Sigma^* / R$ 表示等价关系分开的集合数量，称为$R$关于 $\Sigma^*$ 的指数

$R_M$ 的分割更细致，因此称 $R_M$ 是 $R_{L(M)}$ 的加细

Myhill-Nerode定理：如下三个命题等价

L是RL
L是$\Sigma^*$ 上某一个具有有穷指数的右不变等价关系R的某些等价类的并
$R_L$ 具有有穷指数

证明该语言不是RL最方便的方法就是证明$R_L$的指数是无穷的

例：

证明 $\{0^n1^n|n\geq 0\}$不是RL

极小化DFA

算法步骤

标记终止状态和其余非终止状态可区分
从第一个状态开始迭代标注它与其余状态是否可区分：
1. 如果状态对转移后的关联状态对可区分，那么该状态对可区分
2. 如果关联状态对没有被标注，那么将该关联状态加入关联状态链表（基于一个双向链表实现）（对状态列表的保存有冗余设计，每次向前添加时，实际会新建链表，即如果有一链表 q0->q3->q2，那么 q3->q2，q0->q3->q2都会被保存）
3. 如果迭代到的状态对被标记，那么寻找以该状态对开始关联列表，并将关联列表上之后的状态都标记上
上述步骤会标记完成可区分状态表，接着合并不可区分状态，将不可区分的状态放入一个集合中：
1. 遍历可区分状态表中的所有状态对
2. 如果两状态对不可区分，那么遍历最终的不可区分状态
  1. 如果能在不可区分状态里找到某个集合包含状态对中的一个元素，那么将该状态对元素添加到这个集合中
  2. 如果不能，则从状态对元素新建一个集合，加入不可区分状态中。
对于上述得到的新的可区分状态（每个可区分状态可能包含多个不可区分状态），逐个遍历其中的不可区分状态，得到最终针对新可区分状态的状态转移函数。

正则语言判定定理

定理：DFA $M=(Q, \Sigma, \delta, q_0,F)$ 对应语言为非空的充要条件是：
\[ \exists x \in \Sigma^*, \quad |x|<|Q|, \delta(q_0,x) \in F \]
定理：DFA $M=(Q, \Sigma, \delta, q_0,F)$ 对应语言为无穷的充要条件是：
\[ \exists x \in \Sigma^*, \quad |Q|\leq|x|<2|Q|, \delta(q_0,x) \in F \]
可以联系泵引理

定理：设DFA $M_1=(Q_1,\Sigma,\delta_1,q_{01},F_1)$，DFA $M_2=(Q_2,\Sigma,\delta_2,q_{02},F_2)$，则存在判定M1与M2是否等价的算法。

定理：设L是字母表上的RL，对任意$x\in \Sigma^*$，存在判定x是不是L的句子的算法。

上下文无关语言

定义

派生树：

顶点的顺序：V1，V2是派生树T的两个不同顶点，如果存在顶点v，v至少有两个儿子，使得v，是v的较左儿子的后代，v，是v的较右儿子的后代，则顶点v在顶点v2的左边，顶点v2在顶点v，的右边。

派生树的结果：

派生树T的所有叶子顶点从左到右依次标记为X1，X2，…，X，则称符号串X1X2.…Xn是T的结果。
句型a的派生树：“结果为a的派生树”。·派生树的结果可以是句子，也可以是句型
一个文法可以有多棵派生树，它们可以有不同的结果。

设CFG $G=(V，T，P，S)$，$S\Rightarrow^* \alpha$的充分必要条件为G有一棵结果为$ $的派生树。

定义：

最左派生：$\alpha$的派生过程中，每一步都是对当前句型的最左变量进行替换
左句型：最左派生得到的句型可叫做左句型。
最右归约：与最左派生相对的归约叫做最右归约。

定义：

最右派生：$\alpha$的派生过程中，每一步都是对当前句型的最右变量进行替换
右句型：最右派生得到的句型可叫做右句型。
最左归约：与最左派生相对的归约叫做最左归约。

最右派生、右句型、最左归约又称为规范派生、规范句型、规范规约

二义性

字符串对应两个及以上派生树，则文法有二义性

如果语言L不存在非二义性文法，则称L是固有二义性的，又称L是先天二义性的。

无用符号

能出现字符串的派生过程中的有用，否则无用。

删除无用符号

删除派生不出终极符号行的变量

删除不出现在任何句型中的语法符号

依次使用上述算法(先删派生不出终极符号行的变量，再删不出现在任何句型中的语法符号)就可删除无用符号

空产生式

形如 $A\to \epsilon$

求CFG G的可空变量集

去除空产生式

首先求可空变量集U
构造 $P'$
- $\forall A \to X_1X_2\cdots X_m \in P$ 将 $A\to \alpha_1\alpha_2\cdots \alpha_m$ 放入 $P'$ ，如果$X_i \in U,\quad \alpha_i = X_i\text{ or }\epsilon$ ；如果 $X_i\notin U\quad \alpha_i = X_i$

单一产生式

形如 $A \to B$

消除：用$B$ 的表达式直接代替$A \to B$ 中的B

如果 $A \to \alpha$ 不是单一产生式，就放入 $P_2$
如果 $A \to_G^+ B$ 且$B \to \alpha$ 不是单一产生式，那么 $A \to \alpha$ 放$P_2$

CFG化简

流程

删除无用符号；
删除E-产生式；
删除单一产生式；
当删除单一产生式后，文法中再出现新的无用符号时，再次进行删除无用符号。

CNF 乔姆斯基范式

形式都为 $A \to BC$ 或 $A \to a$

不允许有空产生式和单一产生式

通过CFG构造CNF

首先将化简后的CFG转化为都为 $A \to B_1B_2\cdots B_n$ 和 $A\to a$ 的形式

对于 $A \to aB$ 这类转化为 $A \to A_aB \quad A_a \to a$
将形如 $A \to A_1A_2\cdots A_n$ 都替换为
\[ A \to A_1B_1 \\ B_1 \to A_2B_2\\ \cdots\\ B_{n-2} \to A_{n-1}A_n \]

GNF 格雷巴赫范式

有如下两种形式

$A\to a$
$A\to a A_1A_2\cdots A_m$

首先 $A \to \alpha B \beta$ 又 $B \to \gamma_1|\gamma_2|\cdots$ 那么可以将B替换为$\gamma$

递归

如果存在 $A \Rightarrow^n \alpha A \beta$ 则称为递归派生；n>2 称为间接递归；$\alpha = \epsilon$ 称为左递归，反之为右递归

引理：对于
\[ \left\{ \begin{align} A &\to A\alpha_1|A\alpha_2|A\alpha_3\cdots\\ A &\to \beta_1|\beta_2|\beta_3|\cdots \end{align} \right. \]
可以替换为
\[ \left\{ \begin{align} A &\to \beta_1|\beta_2|\beta_3|\cdots\\ A &\to \beta_1B|\beta_2B|\beta_3B|\cdots\\ B &\to \alpha_1|\alpha_2|\alpha_3|\cdots\\ B &\to \alpha_1B|\alpha_2B|\alpha_3B|\cdots \end{align} \right. \]

CFG转GNF

首先将产生式化成形式（通过引入变量替换终极符）
\[ A \to A_1A_2\ldots A_m\\ A\to a A_1A_2\ldots A_{m-1} \\ A \to a \]
将产生式都转化为形式
\[ A_i \to A_j \alpha\quad i < j\\ A_i \to a \alpha\\ B_i \to \alpha \]

当出现j < i 的情况，就用 $A_i$ 的表达式替换，直到出现左递归:

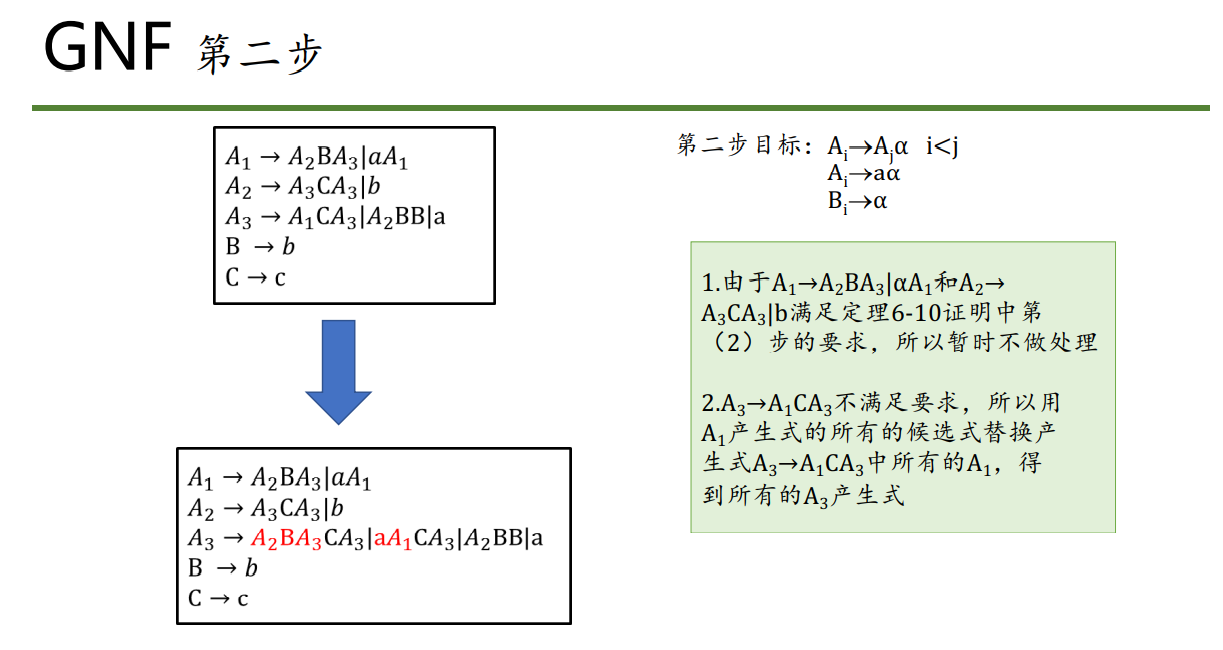
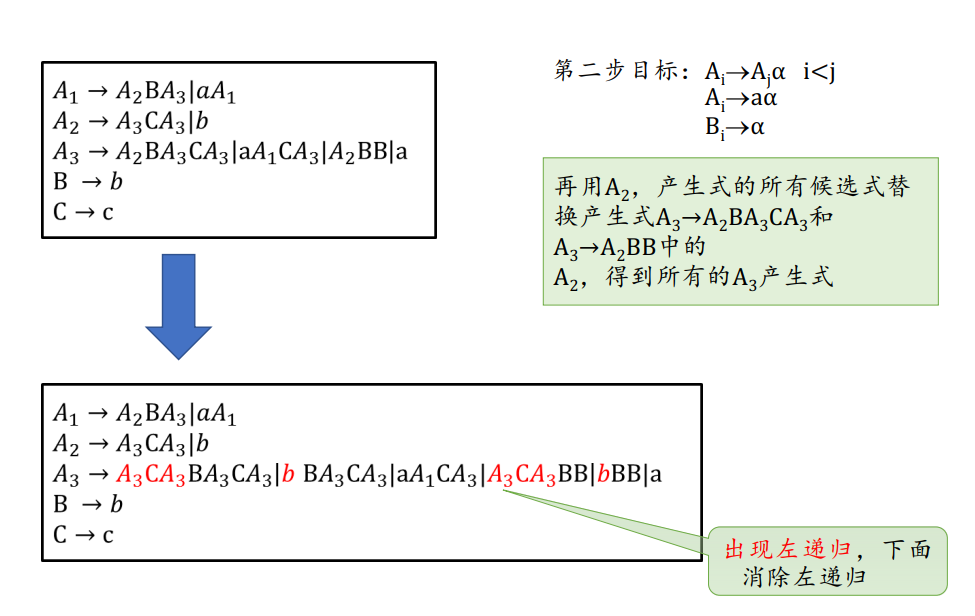
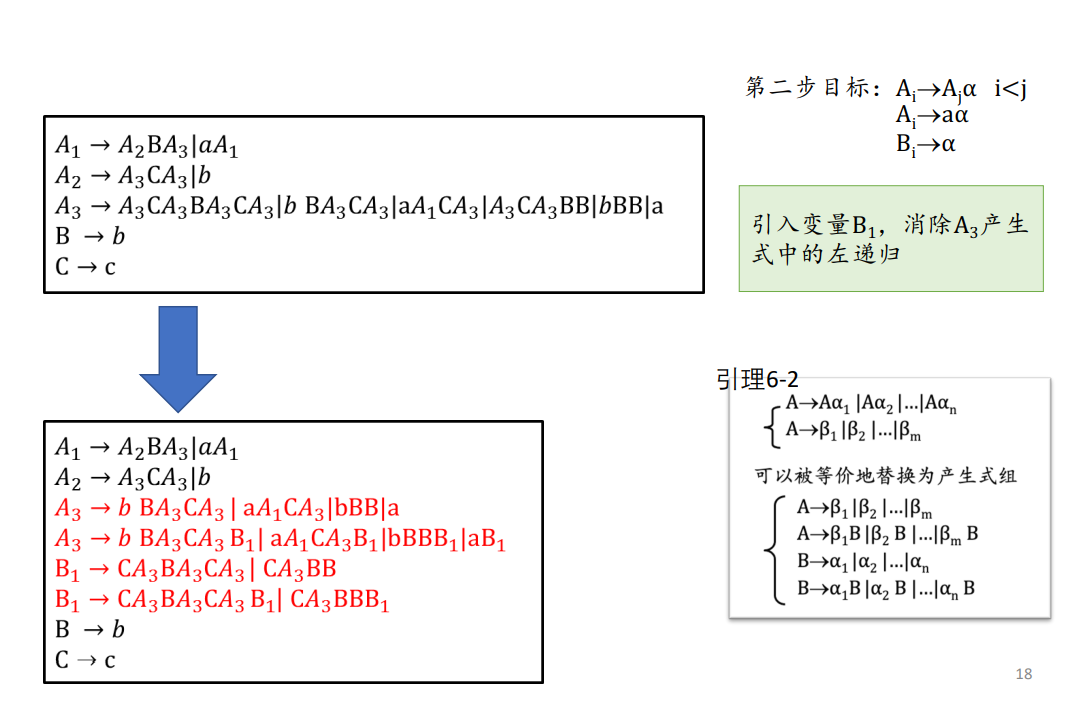
具有最大下标的A已经满足GNF的要求，将这些产生式带入还不满足要求的$A_2$产生式，使得$A_2$产生式都满足GNF的要求；之后递归的带入 $A_1$

下推自动机

CFG都可以化为GNF，最左派生是，句型中变量都以后缀形式出现。

使用下推自动机识别CFG
\[ M = (Q,\Sigma, \Gamma, \delta,q_0,Z_0, F) \]

Q状态集合
$\Sigma$ 输入字母表
$\Gamma$ 栈顶符号表
$Z_0\in \Gamma$ 开始符号，启动时栈内唯一的符号
$q_0$ 开始状态
F终止状态
$\delta$ 转移函数，$\delta: Q \times (\Sigma\cup \{\epsilon\} \times \Gamma) \to 2^{Q\times \Gamma^*}$

\[ \delta(q,a,Z) = \{(p_1, \gamma_1), (p_2, \gamma_2), \cdots\} \]

表示状态q下，栈顶为Z，读入a，状态可以转移为$q_i$ 并且弹出Z并将 $\gamma_i$ 从右至左压入栈，读头移动，准备读入下一个字符。

特别的如果$a = \epsilon$ 那么读头不移动。

同样有 即时描述：$(q,w,\gamma)$ 当前状态q，未处理字符串w，栈内符号串$\gamma$ （最左侧为栈顶）

接收语言

两种接受方法：

转移到特定终态接收记作$L(M)$
空栈接收（栈为空时接收）记作$N(M)$

GNF转PDA

模拟最左派生，对于 $A \to b \alpha$，就是读入b，压栈$\alpha$
\[ \forall A \in V,\ a\in T,\ \gamma \in V^*\\ \delta(q,a,A) = \{(q,\gamma)|A\to a\gamma \in P\} \]
对于含有空串的语言，再加入识别空串的 $\delta_1(q_0,\epsilon, Z) = \{(q_0, \epsilon), (q,S)\}$

类似的还可以终态接受

还可以直接观察语言结构来设计自动机，常用

终态接受的PDA转空栈接受PDA

状态加入初始状态和清栈状态，栈顶符号加入一个用于放在栈底的符号。

初始状态空移动转移到原PDA初始状态，并将新加的栈符号连同原PDA栈底符号压入栈底

之后所有的转移都模拟原PDA，直到原终止状态

原终止状态转移到请栈状态，开始通过空移动清栈。

空栈接受PDA转终态接受的PDA

加入终止状态和标志栈底的元素，等看到栈底元素后就进入终止状态。

PDA转CFG

使用三元组 $[q,A,q_{next}]$ 表示CFG中变量，其中A是栈顶符号。

对于 $\delta(q,a,A) = (q_1,A_1A_2\cdots A_n)$ 我们不确定处理完$A_1$ 到 $A_n$ 后状态是什么，那么就遍历

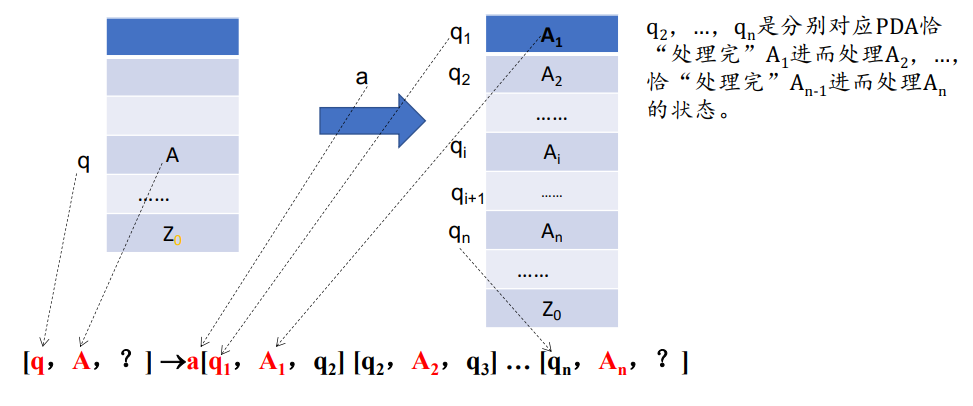
流程：

以该题为例

首先构造S的产生式 $S\to [q_0,Z,q_0]|[q_0,Z,q_1]|[q_0,Z,q_2]$
对每个转移函数构造产生式

对于空串的处理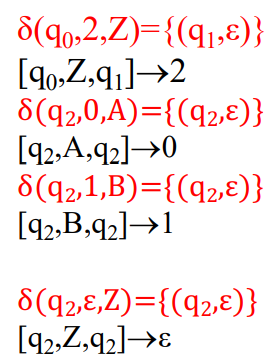

上下文无关语言

CFL的泵引理

$z L $ 当 $|z| \geq N$ 存在u,v,w,x,y，使得 $z = u\ vwx\ y$ 同时满足

$|vwx| \leq N$
$|vx| \geq 1$
$\forall i \in N^+,\quad uv^i wx^i \in L$

利用CFL泵引理证明一个语言不是CFL的步骤：

首先假设该语言是CFL，则其应该满足泵引理，选任意的N.
找到某一个语言中的句子$z\in L(|z|\geq N)$.
分析各种v、x取值，当满足z=uvwxy，且$|vwxl\leq N$，$|vx|\geq 1$时，均能找到一个$i>0$，使$uv^iwx^iy \notin L$.
推出矛盾说明假设不成立，即该语言不是CFL。

需要讨论所有uvwxy的取值

Ogden引理

$z L $ 当z中至少含有N个特异点时，存在u,v,w,x,y，使得 $z = u\ vwx\ y$ 同时满足

$|vwx|中特异点个数 \leq N$
$|vx|中特异点个数 \geq 1$
$\forall i \in N^+,\quad uv^i wx^i \in L$

同样反证的时候利用该定理

封闭性

在并、乘积、闭包运算下封闭

在交、补运算下不封闭

定理：CFL与RL交是CFL

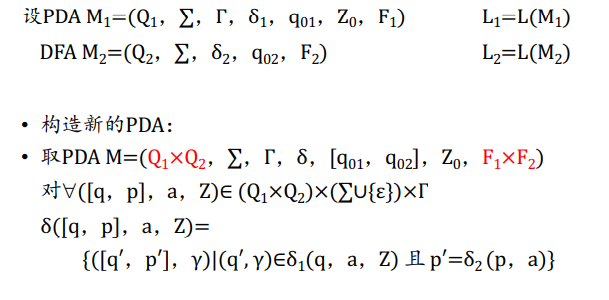
当构造多个语言相关的识别器时可以通过原来的控制器构造，如 $M=(Q_1\times Q_2\times \cdots, \Sigma, \delta, [q_{10}, q_{20}, \cdots], F_1\times F_2\times \cdots)$

代换运算 封闭，参考正则代换有CFG G=(V,T,P,S) $\Sigma$ 是另外的字母表，那么映射 $f:T\to 2^{\Sigma^*}$ 称为代换，$f(a) , \forall a \in T$ 也是CFL

同态运算、逆同态运算封闭

判定算法

判断是否非空

判断是否有穷

可派生性图

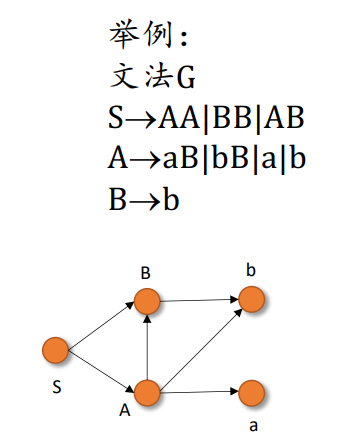
那么对于派生 $A \Rightarrow^+ \alpha A \beta$ 存在的充要条件是：G的可派生性图表示中存在一条从标记为A的顶点到标记为A的顶点的长度非0的有向回路。且回路中的顶点要从S顶点“可达”。

定理：G=(V,T,P,S) 不含无用符号，那么L(G) 为无穷语言的充要条件是：G的可派生性图表示中存在一条有向回路

简化可派生性图

从可派生性图删除终极符号

同样可以判断是否为无穷语言

CFL成员判定问题

x是否为L(G)的句子的判定

CYK算法

基本思想：设给定的文法为CNF文法，对于任意字符串x，如果x的第k个字符a可以由B派生出，并且x的第k+1个字符b可以由C派生出，当$A\to BC\in P$时，ab可以由A派生出

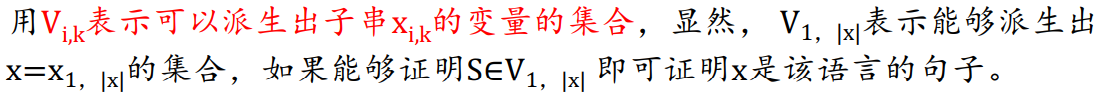
算法具体步骤

k控制字串长度，i控制字串开始位置，j控制将字串切分成两端

图灵机

TM基本模型包括：

一个有穷控制器。
一条含有无穷多个带方格的输入带。
一个读写头。

TM的每次移动与所读符号、所处状态有关。一个移动将完成以下三个动作：

改变有穷控制器的状态；
在当前所读符号所在的带方格中印刷一个符号；
将读写头向右或者向左移一格。

基本的图灵机
\[ M = (Q,\Sigma,\Gamma, q_0, B, F) \]

Q 状态集合
$q_0$ 初始状态
F，终止状态集
$\Gamma$ 带符号表，可以出现在纸带上的符号集合
$B \in \Gamma$，空白符，含有空白符的带方格被认为是空的
$\Sigma \subset \Gamma-{B}$ 输入字母表，只有 $\Sigma$ 中的符号才能在M启动时出现在输入带上
$\delta:Q\times \Gamma \to Q \times \Gamma \times \{R,L\}$ ，RL表示向右向左移动，先改变状态，再将所在的方格中印刷字符Y，最后再移动

特别的，如果遇到转移函数没有定义的情况，图灵机就停机

$\alpha_1 q \alpha_2$ 称为即时描述 (ID)，即时描述移动使用 $\vdash_M$

接受的语言叫做 递归可枚举语言

如果TM对于每个输入串都停机，接受的语言叫做 递归语言

递归语言是递归可枚举语言的子类，而上下文有关文法是递归语言的子类

上下文有关文法CSG

0型文法：短语结构文法PSG，也叫递归可枚举集

1型文法：上下文有关文法

具体见乔姆斯基文法体系

图灵机与PSG等价

线性有界自动机

线性有界自动机（linear bounded automaton，LBA）

非确定的TM。
输入字母表包含两个特殊的符号C和$，其中，C作为输入符号串的左端标志，$作为输入符号串的右端标志。
LBA的读头只能在C和$之间移动，它不能在端点符号C和$上面打印另外一个符号。

LBA与CSG等价

形式语言与自动机复习

字母表

乔姆斯基文法体系

0型文法

1型文法

2型文法

3型文法

正则文法最简形式

线性文法

右线性文法

左线性文法

语言识别

回溯

有限自动机

DFA

即时描述

NFA

从NFA到DFA

带空移动的NFA

由带空移动的NFA构造等价NFA

FA接收的语言是RG

DFA转RG

RG转DFA

左线性文法转DFA

DFA转左线性文法

FA的变形

2DFA

2NFA

Moore机

Mealy机

正则表达式

运算律

RE与FA等价

RE转NFA

加法构造

乘法构造

闭包构造

DFA转RE

正则语言表示方法转化

正则语言的性质

泵引理

利用泵引理证明一个语言不是RL

正则语言的封闭性

正则代换

Myhill-Nerode

极小化DFA

正则语言判定定理

上下文无关语言

二义性

无用符号

删除无用符号

删除派生不出终极符号行的变量

删除不出现在任何句型中的语法符号

空产生式

求CFG G的可空变量集

去除空产生式

单一产生式

CFG化简

CNF 乔姆斯基范式

通过CFG构造CNF

GNF 格雷巴赫范式

递归

CFG转GNF

下推自动机

接收语言

GNF转PDA

终态接受的PDA转空栈接受PDA

空栈接受PDA转终态接受的PDA

PDA转CFG

上下文无关语言

CFL的泵引理

利用CFL泵引理证明一个语言不是CFL的步骤：

Ogden引理

封闭性

判定算法

判断是否非空

判断是否有穷

可派生性图

简化可派生性图

CFL成员判定问题